泊松过程（Poisson Process）在上大学学排队论的时候就学过，但是当时感觉就没搞太清楚，最近又看了一遍，感觉似乎理解了一些东西，这篇博文会不定期更新，以添加我最新的理解。

先说说泊松分布

讲之前首先强调一下，泊松分布（Poisson Distribution）和泊松过程是两个概念。泊松分布是一种概率分布，一种概率分布说白了就是一类具有相同形式的概率密度函数。而泊松过程是指一个随机过程，随机过程可以看做是在一个连续或者离散的时间线上，连续发生的一系列随机事件的组合。所以泊松分布和泊松过程并不是一码事。

另外，泊松过程也不是说这个过程中的每一个随机事件符合泊松分布。泊松过程是一个比较抽象的过程，这也是为什么我学了这么长时间一直没理解清楚的原因（我觉得是这样/捂脸/）。至于它到底是个什么样的过程，等会我再说。

泊松分布

咳咳，好吧，现在开始真的说泊松分布啦~

为了引出泊松分布，我们先说伯努利分布（Bernoulli distribution），又叫0-1分布，如果一个离散变量只能取0、1两个值，那么就说这个变量服从伯努利分布：

\eqc P(x=k) = \left\{\begin{aligned} & 1 - p, & k = 0 \\
& p , & k = 1 \end{aligned}

举个例子，你抛一枚硬币（这个硬币不一定两面是一样重的，跑出两面的概率不一样），会得到正面（1）或者反面（0）两个结果，这个时候你的结果的分布就服从伯努利分布。其实这个很好理解对吧……

然后说二项分布，如果你做n次互相独立同分布的伯努利实验，那么各次实验结果的和（也就是结果为1的次数）将会服从二项分布。二项分布的概率函数为：

\eqc P_n(x) = C_n^x \cdot p^x \cdot (1-p)^{(n-x)}

诚然，当\eq n=1时二项分布即为伯努利分布。

真的真的要说泊松分布了

泊松分布是二项分布的另一个极限情况，当二项分布中的阳性概率\eq p \rightarrow 0很小而试验次数\eq n \rightarrow +\infty时，满足\eq np = \lambda时，得到的即为参数为\eq \lambda的泊松分布，所以泊松分布的概率函数为：

\eqc P(x) = \mathop{lim}\limits_{n \rightarrow +\infty} P_n(x) = \lambda^{-x} \cdot \frac{e^\lambda}{k!}

可以证明，泊松分布的期望和方差都是\eq \lambda。

从上面的推导来看，泊松分布所表达的其实是这么一件事，就是说当你做有限次的伯努利实验时，发生阳性结果（至少发生一次）的概率近乎于0，但是当你做无穷多次的时候，阳性结果发生的概率就不是0了，而是一个随机的有限的值（期望是有限的）。这样说似乎很奇怪，因为现实世界中似乎并没有这样奇怪的实验去做。

如果你觉得上面这段话不好理解，那我给你举个反面的例子，你可以从相反的方向理解一下（当然这段话并不重要，所以你可以不看），但是请注意，以下并不是泊松分布的真正意义。工程界有一个著名的定律叫做墨菲定理，它的说法大概是说：“如果一件事情有变坏的可能性，那么它就一定会变坏”。这句话似乎非常匪夷所思，它是一个叫墨菲的工程师提出的，我觉得他说这句话的本意只是提醒其他的工程师要注意细节，再小的bug都不要忽视。

不过，它之所以被称为“定理”，的确是有它的科学依据的，让我们来假设“变坏”是一个阳性结果（1），那“正常”就是阴性结果（1），“一件事情有变坏的可能性”也就是说存在一个\eq p \not= 0，那么你对\eq P_n(x)求\eq n \rightarrow \infty的极限会发现，当\eq x = 0时\eq P_n(x) \rightarrow 0，也就是说这件事情不变坏的可能性为0，也就是说它一定会变坏咯，所以墨菲定理其实是有数学依据的。当然根据这个推导你也可以看出，\eq P_n(n)其实还是0，实际上应该说在长期的生产中一定不会一直正常，但也一定不会一直出故障。墨菲想说的是，虽然不会一直出故障，但一定会出故障，但有些故障是绝不允许发生的，所以你得让\eq p = 0。

实际中你不可能让\eq p = 0，但你可以做到让\eq p \rightarrow 0，也就是说，你可以让事件发生的次数服从一个泊松分布，这个时候事件不发生的概率就不再趋近于0了，而是有一个确定的概率值，实际上事件发生\eq x次的概率值都是确切的，而当\eq x \rightarrow +\infty时，概率将会趋近于0.

泊松过程

这篇文章重点在于讲泊松过程，这一段我着重给出泊松过程的一些数学上的定义和推导，后面会慢慢讨论的。

首先讨论增量过程，如果随机变量随着时间的变化其值会增加，则这个过程就是一个增量过程，增量\eq X(t_2) - X(t_1)是一个随机变量。数学表示就是\eq X(t_2) - X(t_1) > 0, \ \forall\ 0<t_1<t_2.

在一个增量过程中，如果对于任意的\eq 0<t_1<t_2<t_3<t_4，增量\eq X(t_2) - X(t_1)和\eq X(t_4) - X(t_3)是独立的，那么这就是一个独立增量过程。也就是说，独立增量过程中，任意两个不重叠的时间段之内的增量是独立的。

在一个独立增量过程中，如果对于任意的\eq t_1,t_2,h > 0，增量\eq X(t_2) - X(t_1)和\eq X(t_4 + h) - X(t_1 + h)服从相同的分布，那么这个过程就是一个平稳增量过程。

在平稳增量过程，对于一个给定的时间间隔\eq \tau，如果增量\eq X(t+\tau) - X(t)服从泊松分布，那么这个过程就叫做泊松过程。

下面给出泊松过程的定义：如果单位时间内事件发生的次数\eq X符合泊松分布\eq P(X=k) = \frac{e^{-\lambda} \lambda^k}{k!}，则这个随机过程是一个参数为\eq \lambda的泊松过程。

理解泊松过程的含义

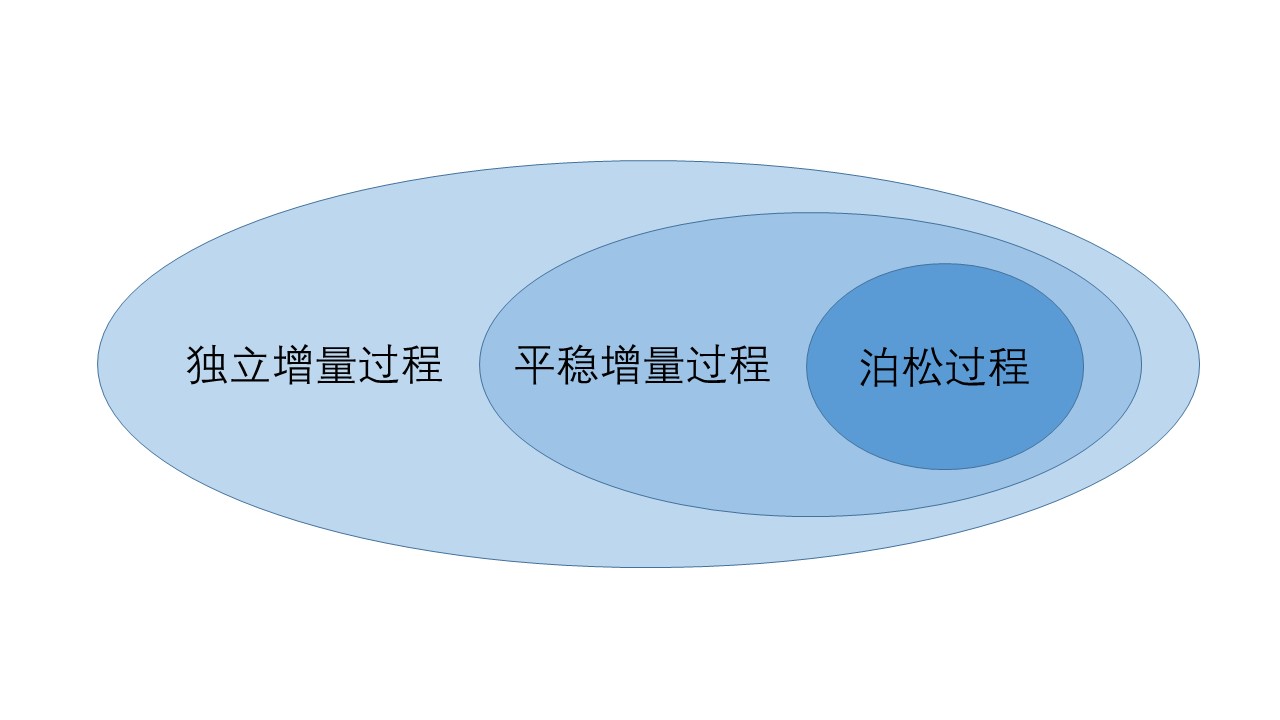
上面啰嗦了那么多，主要是为了讲清泊松过程的来历，从上面的推论看出，泊松过程实际上就是描述这么一个过程，在每一刻，某个事件发生的概率是确定的，而在固定的时间段之内，发生这个事件的次数服从一个特定的概率分布。但是，这样的一个过程不一定是泊松过程，它实际上是一个平稳增量的过程，而泊松过程的实际上是一类特定的平稳增量过程，增量的分布服从泊松分布的平稳增量过程才是泊松过程。

关于泊松过程的参数\eq \lambda的含义

\eq \lambda的正式定义是到达率，它指的是单位时间内发生事件次数的期望值，对于任意的时间间隔\eq \tau，在这段时间内发生事件次数实际上也符合泊松分布，这个泊松分布的参数是\eq \lambda\tau。